Польза кубика рубика в изучении математики

«Ненавижу математику». За этой нелюбовью школьников может скрываться «мне скучно», «я не понимаю», «не представляю, где она мне пригодится». Дэн Ван дер Вирен, учитель математики и любитель головоломок из США, решил бороться со всеми возражениями сразу. В июне 2018 он выступил с докладом «Использование кубика Рубика для улучшения STEAM образования» на конференции TED, миссия которой состоит в распространении уникальных методов и креативных идей обучения. С тех пор Дэн продолжает делиться своими педагогическими успехами, и, судя по ажиотажу вокруг этой темы, он не единственный, кто принес кубики в класс. Как и для чего можно использовать кубик Рубика на уроках и факультативных занятиях по математике, рассказываем в нашей статье.
Немного истории
Первым, кто попытался связать игру по сбору цветов в определенные группы с математикой, был, конечно, сам Эрно Рубик, профессор архитектуры из Венгрии. Он создал кубик в середине 70-х годов прошлого века, чтобы наглядно объяснить своим студентам теорию групп.
С того времени по всему миру было продано более 350 миллионов кубиков, что делает их рекордсменами среди игрушек. Кубик Рубика адаптирован даже для незрячих – существует версия с рельефными гранями.
В авангарде всемирного увлечения головоломкой шли школьники и студенты. И хотя кубик уже пережил первую волну популярности, по-видимому, приближается вторая.
Если вам никогда не давалась эта головоломка, не отчаивайтесь. Самому Рубику пришлось потратить почти месяц на то, чтобы справиться со своим изобретением.
Где же тут математика
Связь между кубиком Рубика и математикой заметить несложно. Он может использоваться, например, для осмысления площади и объема, для наглядного объяснения таких понятий, как дроби, отношения и пропорции.
Вариант задачки:
Пусть на одной стороне перемешанного кубика три красных, один синий, два зеленых, два желтых и один оранжевый квадрат. Учитель может спросить: «Какую часть занимают красные квадраты?»
Ответ: 3/9 или 1/3
В книге Александра Юрьевича Эвнина «150 красивых задач для будущих математиков» приводится такое упражнение: «Через центр кубика Рубика провели плоскость, перпендикулярную его диагонали. Сколько маленьких кубиков пересекла эта плоскость?» Решение задачи требует особой внимательности. Плоскость пересекает 19 кубиков.
Задачка для факультатива
На факультативных занятиях по математике в старших классах учитель может разобрать концепцию факториалов, подсчитав число возможных состояний кубика Рубика. А это целых 43 252 003 274 489 856 000 расстановок! Тот факт, что из любого состояния кубик Рубика можно собрать за 20 ходов, обычно вызывает неподдельное любопытство у школьников.
Чтобы не отпугнуть учеников сложностью задачи, для начала можно предложить им просто заполнить пропуски в карточках (для удобства правильные ответы выделены жирным):
Существует всего 8 угловых кубиков, которые могут находиться в 8 разных местах на большом кубе. Мы можем определить их местоположение 8! возможными способами (поставить первый кубик на одно из 8 свободных мест, второй – на одно из оставшихся 7 мест и так далее 8*7*6*5*4*3*2*1=8!)
Каждый из 8 угловых кубиков можно повернуть одним из 3 способов, получается, что существует всего 38 вариантов.
Таким образом, общее количество возможных расположений угловых кубиков составляет (8!) (38), что равняется 264 539 520
Шаг за шагом класс сможет приблизиться к пугающим 43 квинтиллионам в ответе.
Опыт Дэна Ван дер Вирена
Дэну Ван дер Вирену повезло работать в маленькой американской школе, где ученикам было от 14 до 20 лет, а администрация поощряла творческий подхода к обучению. На его уроках впервые появились кубики Рубика.
Я спрашивал себя, — вспоминает Дэн, — как изменилось бы отношение учеников старших классов к математике, если бы они имели возможность познакомиться с той ее стороной, которая включает практические действия, командную работу и заканчивается достойным гордости результатом?
Первым нестандартным шагом на уроках стали неформальные беседы и обсуждения способов сбора кубика по цветам. По мере того, как ученики работали с кубиками, Ден предлагал все более сложные темы для математических бесед.
В разные дни он задавал ученикам такие вопросы: «Какой процент головоломки закончен?» или «Если каждый из вас способен собрать одну сторону в среднем за две минуты, то сколько времени потребуется для полного сбора кубика?» Школьники, привыкшие к обсуждениям, охотно решали завуалированные задачки. Дэн стремился создать на уроках непринужденную атмосферу, класс не пользовался даже тетрадями и ручками.
Идеи для учителя
Одна из 4 секций шаблонов мозаики «Портрет Анны Франк» (в каждой секции 25 шаблонов). Источник фото: youcandothecube.com
Сложно представить занятия с кубиком как альтернативу урокам в наших школах, но использование этой умной игрушки может повысить шансы заинтересовать математикой тех учеников, которые не преуспели по этому предмету при использовании традиционных методов обучения.
Вдохновение для уроков можно найти на сайте You Can Do the Rubik’s Cube. Здесь учителя со всего мира делятся своими наработками и методиками, например, в одном из материалов описано, как собрать мозаику из кубиков Рубика, чтобы получилось изображение Анны Франк.
Кубик Рубика является самой известной головоломкой прошлого столетия. У каждого второго подростка в нашей стране была такая игрушка. Сегодня она вновь возвращает былую популярность, во всем мире проводятся конкурсы по ее сборке на скорость. Многие родители задумываются о курсах, обучающих детей спидкубингу. Поговорим о том, что это такое, и в чем польза таких занятий.
Школа спидкубинга
Кубик Рубика был придуман и сконструирован архитектором и скульптором Эрно Рубиком в 1970 году. Он стал одной из самых популярных игрушек двадцатого века. Сначала родители и учителя воспринимали кубик Рубика как простую игрушку, отвлекающую детей от учебы. Позже эта головоломка завоевала умы миллионов людей по всему миру. На сегодняшний день сборка кубика Рубика популярнейший вид интеллектуального спорта. Существует даже международная ассоциация, которая регулярно проводит соревнования и ведет свой рейтинг достижений спортсменов.
Многие родители, глядя на поразительные результаты при решении этой головоломки, задумываются о том, чтобы научить своих детей сборке кубика Рубика. Конечно, в век высоких технологий можно освоить этот навык и самостоятельно. Но занятия через интернет могут быстро наскучить малышу, и он, потеряв мотивацию, перестанет тренироваться. По этой причине лучшим вариантом является посещение специальных курсов, обучающих спидкубингу (speedcubing, от англ. speed скорость, и cube куб) быстрой сборке кубика Рубика. Подобное обучение не только позволит постепенно освоить различные тактики решения головоломки, но и разовьет множество полезных навыков.

Что развивает кубик Рубика у детей
Кубик Рубика это уникальная головоломка. Помимо того, что его сборка достаточно интересное и увлекательное занятие, она развивает множество полезных навыков и качеств, с которыми любая задача станет ребенку по плечу:
Мелкая моторика
Для того, чтобы собрать головоломку, приходится выполнять огромное количество механических действий. Передвигая ряды вверх и вниз, вправо и влево, постепенно наращивается скорость. Движения становятся выверенными, точными и доведенными до автоматизма. Таким образом, развивается не только подвижность пальцев, но и общее умение ими управлять. В дальнейшем это поможет ребенку легче справляться с мелкой и требующей точности работой.
Концентрация
Решение такой сложной головоломки требует предельной внимательности и усидчивости. За подобным занятием малыш сам не замечает, как приобретает умение концентрироваться на решении конкретной задачи. Это положительно сказывается на учебе в школе, ведь там также очень важна сосредоточенность как при выполнении заданий, так и на теме урока.
Память
Хорошая память в современной жизни просто необходима, ведь чем она лучше, тем легче дается учеба или работа. Важно развивать память с самого детства, и кубик Рубика с этой задачей справляется просто отлично. Для решения головоломки ребенку приходится запоминать множество различных способов, держать в уме огромное количество комбинаций. Таким образом, у него заметно улучшаются все виды памяти, что позволяет легче учиться в школе.
Скорость реакции
Если в начале занятий ученики хотят просто добиться решения головоломки, то потом они стремятся сложить ее за минимальные сроки. Постепенно время между решением, какие грани повернуть, и самим действием сокращается. По завершению курса обучения, вырабатывается практически мгновенная скорость реакции.
Стратегическое мышление
Собрать кубик Рубика можно множеством различных способов. Малыш учится использовать разные техники, и, в зависимости от ситуации, выбирает оптимальные. Это формирует у него стратегическое мышление: способность выстраивать тактику на много ходов вперед, мгновенно оценивать обстановку, выбирать самый простой путь для решения задачи в минимальные сроки.

Пространственное мышление
Для решения данной головоломки просто необходимо представлять ее в уме. Это улучшает пространственное мышление. Когда оно хорошо развито, человеку удается легче справляться с геометрическими и техническими задачами. Неизвестно, какую профессию выберет ребенок, но если она напрямую или косвенно будет связана с визуализацией, то занятия спидкубингом в детстве дадут ему хорошую базу для подобной работы.
Логика и анализ
Становление причинно-следственных связей, выбор правильной последовательности действий, быстрый анализ ситуации и принятие верного решения это не полный список того, за что отвечает логическое мышление. При сборке кубика Рубика используются и развиваются все эти навыки, что приводит к лучшему пониманию и освоению как точных, так и гуманитарных наук.
Польза кубика Рубика для ребенка
Помимо разностороннего развития умственных способностей, сложение кубика Рубика несет в себе массу других положительных свойств. Главным из них по праву можно считать снижение уровня стресса у детей. Современные школьники усваивают огромные объемы информации, программа обучения требует от них серьезной отдачи. По этой причине дети часто подвержены стрессу, что вредит их формирующейся психике. А механические действия при сборке головоломки отвлекают и успокаивают малыша. По такому же принципу работают современные спиннеры, а также известные нам с древности четки.
Во время решения головоломки ребенок учится преодолевать трудности, а добиваясь успеха, приобретает уверенность в собственных силах. Особенно заметно, как повышается самооценка у скромных и тихих детей. Целеустремленность это то качество, которое трудно привить ребенку, а в данном случае малыш сам воспитывает в себе стремление добиваться цели.
К еще одному положительному свойству занятий по сборке кубика Рубика можно отнести улучшение речи, ведь за нее отвечает то же полушарие мозга, что и за моторику рук.

Курсы спидкубинга
Обучать спидкубингу можно с раннего возраста, но специалисты рекомендуют приступать к занятиям не раньше шести-семи лет. К этому времени детский мозг уже способен решать логические задачи.
Выбирая курсы спидкубинга, необходимо обратить внимание на методику обучения. Такой кружок должен вестись по определенной программе, включающей себя различные тактики и способы собрать головоломку. Ведь последовательный подход позволяет добиться хороших результатов.
Для юных учеников занятия должны проходить в игровой форме, так им не наскучат тренировки. Чтобы педагог смог уделить внимание каждому ученику, необходимо обучать детей в небольших группах.
Существует множество различных кружков, на которых малышей научат собирать эту замечательную головоломку. Одной из самых известных в России школ интеллектуального развития детей и подростков, в которой обучают спидкубингу, является академия AMAKids, где лучшие педагоги помогут малышу освоить сборку кубика Рубика. Здесь ученики приобретут множество полезных навыков и умений, которые пригодятся им и в школе, и во взрослой жизни.
Что может быть интереснее, чем собирать кубик Рубика на скорость? А если сложить 100 кубиков, может получиться портрет Мэрилин Монро. Дан ван дер Вирен, учитель математики средней школы в США, придумал, как связать математику с реальной жизнью и начать использовать на уроках кубик Рубика.
Привет, учитель! Рассылка
Для тех, кто работает в школе и очень любит свою профессию
«Я не люблю математику», — обычно говорят мои ученики. В альтернативной средней школе в Колорадо, где я работаю последние два с половиной года, учатся дети от 14 до 20 лет. Они приходят к нам, если им сложно в традиционной школе, потому что мы в основном используем творческие методы обучения.
Размышляя над словами учеников, я спрашивал себя: «Как изменилось бы их отношение к математике, если бы появилась возможность увидеть другую её сторону? Если бы она включала практическое обучение, способствовала командной работе и закончилась бы проектом, которым можно гордиться?» Основываясь на собственной любви к популярной головоломке, я решил использовать кубик Рубика в целях сплотить моих нетерпимых к математике учеников и привить им любовь и интерес к предмету.
Я прочитал о детях, которые собирают из кубиков портреты исторических личностей, популярные достопримечательности и животных, и увидел в этом способ стимулировать критическое мышление и алгоритмическое решение проблем.
Связь между реальностью и математикой
Пока дети собирали кубики, я свободно беседовал с ними о математике. И как только ученики успешно собирали одну из граней, им становилось всё интереснее обсуждать головоломку.
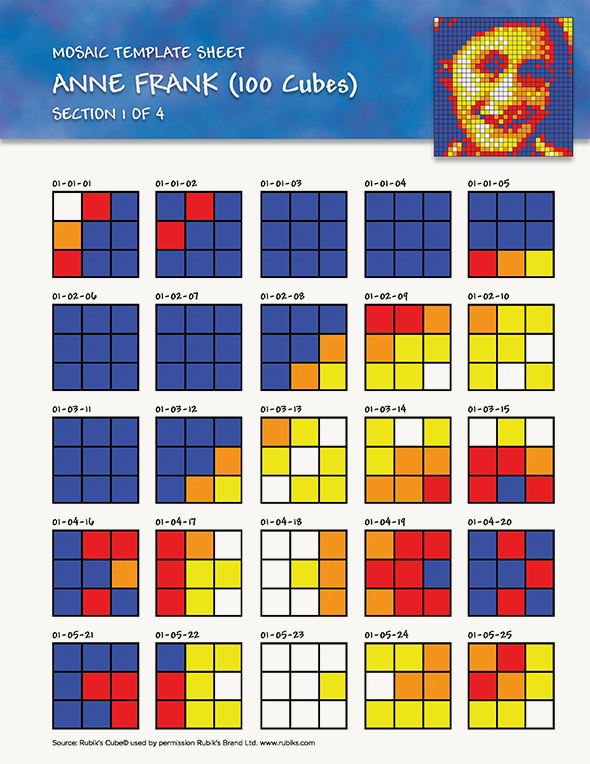
Ученики делают мозаику из 100 кубиков, где каждый должен соответствовать определённому шаблону (на схеме шаблоны для 25 кубиков)
По прошествии пары дней я задавал детям вопросы: «Какой процент мозаики закончен?» или «Если каждый из трёх учеников способен собрать одну грань в среднем за две минуты, сколько времени потребуется для завершения мозаики?»
Я хотел дать моим ученикам возможность использовать навыки оценки и рассуждения параллельно с тем, как они получают положительные эмоции от самого процесса сборки кубика. Мы ничего не записывали — я хотел, чтобы дети научились мыслить и оценивать свои возможности. По сути, применяли все те полезные навыки, которые помогут им в изучении математики.
Между кубиком Рубика и математикой есть связь
Например, кубик Рубика можно использовать как для того, чтобы обозначить плоскость, так и для того, чтобы продемонстрировать трёхмерность. Он может быть полезен при изучении дробей, коэффициентов и пропорций. Например, на одной грани кубика Рубика могут быть три красные, одна синяя, две зелёные, две жёлтые и одна оранжевая плитки. Учитель может спросить: «Какую часть от видимой грани составляют красные плитки?» (Ответ: 3/9 или 1/3).
Для старшей группы учитель может ввести понятие факториалов, чтобы объяснить, что значат 43 252 003 274 489 856 000 различных комбинаций кубика Рубика. Независимо от того, как кубик устроен, его можно собрать за 20 ходов или меньше — факт, который обычно вызывает любопытство у студентов.
Расположив квадраты из 9, 16 и 25 кубиков Рубика так, чтобы их углы образовывали треугольник, учитель может объяснить и наглядно показать теорему Пифагора — a2 + b2 = c2.
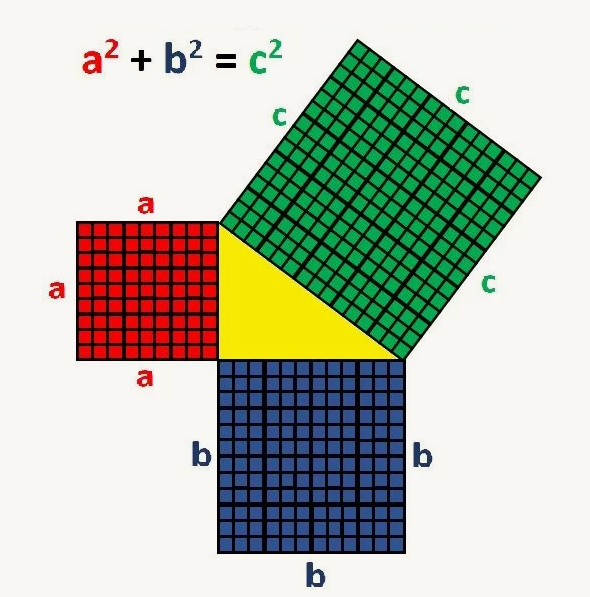
С помощью кубика Рубрика можно объяснить теорему Пифагора
Мозаики из кубика Рубика
Когда я искал способы представить кубик Рубика ученикам, я наткнулся на одну интересную технику его сборки. На сайте You Can Do the Rubik’s Cube есть бесплатные шаблоны для мозаик, когда в итоге картинка из множества кубиков складывается в портрет Анны Франк, или мост Золотые Ворота, или различных животных (там же можно найти руководство по сборке индивидуальных мозаик.) В одной картине может быть задействовано до 600 кубиков.
Здесь же вы можете найти множество руководств по сборке и материалы, которые помогают научить детей решать головоломки и прививать интерес к математике и естественным наукам. Преподаватели в США и Канаде за два месяца используют до 600 шаблонов сборки кубиков Рубика.
В нашей школе есть пятинедельные факультативные курсы, которые мы проводим в зависимости от интересов студентов и учителей. Я решил внедрить изучение сборки кубика Рубика в свой курс. Я назвал его «Искусство и разнообразие решения проблем с кубиком Рубика», а затем арендовал 225 кубов, как только курс был одобрен.
Ученики заинтересовались тем, что можно делать портреты исторических личностей с помощью мозаик. Они делали портрет по своему выбору, а затем изучали подробности биографии этого человека. Среди известных фигур были Мэрилин Монро, Роза Паркс и Никола Тесла.
После того как ученики узнали, как собрать кубик Рубика, большинство из них могли собрать одну сторону за две или три минуты, а иногда даже близко к одной минуте. Они работали в одиночку или с партнёром, чтобы построить одну секцию из 25 кубов за раз. Сбор мозаики из 100 кубиков обычно занимал от 20 до 30 минут, если участвовали пять или шесть учеников.
Как использовать кубик Рубика каждый день
В интернете можно найти бесплатные концепции уроков и отдельных тем для разных предметов. Многие из них созданы для учителей, которые преподают математику и естественные науки.
Например, этот план урока биологии в средней школе предлагает ученикам создать собственных животных, используя генетический код ДНК: «Разработайте и используйте модель для описания того, почему структурные изменения генов (мутации) могут влиять на белки и приводить к вредным, полезным или нейтральным эффектам на структуру и функцию организма».
На сайте есть и блок с девятью уроками, который исследует концепции машиностроения и дизайна, генетики, геометрии форм и фигур, геометрии твёрдых тел и нейробиологии.
Кубик Рубика — это интересный способ изучения многих тем в различных областях. Изменяя привычный образ мышления и развивая умение принимать решения, преподаватели могут вдохновить учеников искать неординарные способы решения проблемы и учат их мыслить критически.
Муниципальное общеобразовательное учреждение
«Орлинская средняя общеобразовательная школа»
Исследовательская работа
Кубик Рубика – детская игрушка
или сложная математическая головоломка
Автор: Кондобаева Валерия
учащаяся 6 класса
МОУ Орлинская СОШ
Руководитель: Угланова О. Г.
учитель математики
Свободный – 21
2018
Оглавление
Введение……………………………………………………………………………3
Глава 1 История создания математического кубика……………………………4
Немного из биографии Эрно Рубика……………………………………..4
История создания магического кубика……………………………………4
Разновидности математического кубика…………………………………6
Алгоритм сборки кубика Рубика 3х3……………………………………..6
Рекорды по сборке кубика Рубика……………………………………….12
Заключение……………………………………………………………………….13
Список литературы………………………………………………………………14
Приложения………………………………………………………………………15
Введение
В начале учебного года в кабинете математике появилась всем известная детская игрушка «Кубик Рубика». Кубик вызвал живой интерес у учащихся 8 класса и моих одноклассников. На переменах кто-то негодовал в неудачной попытке его собрать, а кто-то разбирал на составные части и складывал грань кубика из одного цвета, при этом ликуя – «Я собрал!»
Вот тогда-то я и задалась вопросом: «А что это за игрушка? Почему ее принесли в кабинет? А можно ли этот кубик вообще собрать?»
Проведя анкетирование среди учащихся нашей школы, я увидела следующие результаты (Приложение 1, 2).
Актуальность исследования: при сборке кубика развивается терпение, концентрируется внимание, следовательно, улучшается развитие логического и математического мышления.
Предмет исследования: развитие логического мышления, концентрации внимания, развитие пространственного воображения
Объект исследования: кубик Рубика
Цель исследования: научиться собирать кубик Рубика 3х3х3.
Задачи исследования:
Познакомиться с биографией создателя кубика Рубика
Изучить историю создания кубика Рубика.
Изучить разновидность головоломок Рубика.
Изучить алгоритм сборки кубика Рубика.
Изучить мировые рекорды по сборке кубика Рубика.
Гипотеза исследования: не зная математики можно собрать кубик Рубика.
Методы исследования:
Теоретический: теоретический анализ и обобщение интернет – источников и научной литературы.
Эмпирический: опрос-анкетирование школьников.
Глава 1. История создания математического кубика
Немного из биографии Эрно Рубика.
Эрно Рубик родился в Венгрии в городе Будапеште 13 июля 1944 года во время Второй мировой войны. Его отец был авиаинженером на заводе, а мать — поэтесса.
В 1967 году окончил инженерный факультет Будапештского университета технологии и экономики по специальности инженер – строитель, продолжил обучение в аспирантуре на скульптора и дизайнера интерьера.
В 1971 — 1975 годах работал архитектором, затем снова вернулся в академию и получил звание доцента Будапештского института декоративного и прикладного искусства. В начале 1980-х устроился работать редактором журнала игр и головоломок «És játék» (перевод с венгерского «… и игры»). В 1983 году он открыл свою студию «Rubik Stúdió», которая разрабатывала дизайны интерьеров, мебели и в том числе – головоломки.
В 1987 году получил звание профессора, в 1990 совместно с Яношем Гинстлером основал венгерскую техническую академию и был её президентом до 1996 года. В академии был создан международный фонд Рубика для поддержки особенно талантливых молодых изобретателей.
В настоящее время в основном участвует в разработке видеоигр, пишет статьи по архитектуре и возглавляет студию Рубика.
Что такое кубик Рубика. История его изобретения.
Кубик Рубика (разговорный вариант «Кубик-рубик» первоначально был известен как «Магический кубик») — механическая головоломка, изобретённая в 1974 году (и запатентованная в 1975 году) венгерским скульптором и преподавателем архитектуры Эрно Рубиком.
Головоломка представляет собой пластмассовый куб в первоначальном варианте 3×3×3. Его видимые элементы снаружи выглядят как 54 грани малых кубиков, составляющих один большой куб, и способны вращаться вокруг 3 внутренних осей куба. Каждая грань состоит из девяти квадратов и окрашена в один из шести цветов, в одном из распространённых вариантов окраски расположенных парами друг напротив друга: красный — оранжевый, белый — жёлтый, синий — зелёный; но в различных вариантах кубика Рубика грани окрашиваются в разные цвета совершенно различным образом. Повороты граней позволяют переупорядочить цветные квадраты множеством различных способов. Задача игрока заключается в том, чтобы собрать кубик Рубика: поворачивая грани куба, вернуть его в первоначальное состояние, когда каждая из граней состоит из квадратов одного цвета.
В 1970 году Эрно Рубик, работая преподавателем архитектуры, считал, что студентам будапештской Академии прикладных искусств и ремесел для развития пространственного мышления необходимо хорошо понимать геометрию, различные виды моделирования и математику.
Существуют различные версии того, зачем Рубик решил создать такую интересную модель из кубов: одной из них является та, что Эрно хотел при помощи данного изобретения продемонстрировать своим студентам основы математической теории групп. Идея кубика вынашивалась долгое время, а первоначальная задача была во много раз труднее и практически непосильна – Эрно хотел, чтобы отдельные кубики могли вращаться и не нарушать при этом всей конструкции. К тому же в его задумке у кубика должно было быть 27 кубов с разноцветными гранями, то есть всего27*6=156 граней. В конечной версии все же их осталось 54 – как у современного кубика. Испытать кубик Рубика первым посчастливилось студентам Рубика. Но вскоре, как и у него самого, так и у «испытателей» появилась проблема: как же его все таки собрать?Говорят, после создания кубика, Эрно потратил на его сборку и разработку алгоритма около месяца!
Разновидность головоломок Рубика.
Эрно Рубик изобрел большое количество головоломок, причем некоторые из них имели форму геометрической фигуры (Приложение 3).
Алгоритм сборки кубика Рубика 3х3.
Существует множество способов решить известную головоломку, но простые и понятные схемы для новичков найти не так просто. С каждым пройденным этапом сборки, формулы кубика Рубика 3х3 становятся сложнее. Нужно не только правильно изменить узор, но и сохранить то, что сделано до этого. Ниже будет приведен один из вариантов, как легко собрать кубик Рубика 3х3. Условно весь процесс можно разбить на следующие этапы:
1.Сборка креста в верхней грани кубика.
2. Правильное составление всей верхней грани.
3. Работа над средним слоев.
4. Правильная сборка ребер последнего ряда.
5. Сборка креста нижней грани.
6. Сборка граней одного цвета
Решение головоломки – подготовительная работа
Первый этап самый легкий. Новички могут попробовать свои силы и потренироваться в составлении узоров кубика по имеющимся инструкциям, но этот процесс займет много времени. 
Нужно выбрать верхнюю грань и цвет, который будет собираться первым. Алгоритм сборки кубика Рубика 3х3 для начинающих разработан с позиции “крест”. Сделать его несложно, необходимо выбрать центральный цвет, найти 4 реберных элемента того же оттенка и поднять их на выбранную грань. Цветная стрелочка на картинке указывает на искомую часть. Варианты расположения нужного элемента могут быть разными, в зависимости от этого описаны 2 последовательности действий А и Б. Трудность заключается в том, чтобы продолжить крест по боковым сторонам кубика.
Работа над средним рядом.
На этом этапе схемы сборки кубика Рубика 3х3 для начинающих необходимо найти и собрать угловые элементы верхней грани. В конечном результате должна быть полностью решена грань с крестом и верхний ряд головоломки.
На изображении приведены три случая возможного узора граней. Выбирая один из способов А, Б или В необходимо собрать все 4 угла кубика. Запоминая алгоритмы вращения и отрабатывая их, приобретаются навыки и мастерство сборки головоломки. 
Третий этап кажется простым, но это только видимость. 
Для его решения описаны две ситуации узоров и соответственно составлены две формулы вращения. Применяя их, стоит помнить о сохранении ранее достигнутых результатов. Мастера постоянно держат в памяти 3-4 последних вращений, чтобы в случае неудачи вернуть кубик к первоначальному состоянию.
Для решения головоломки ее нужно вращать по оси координат в поиске необходимых элементов и работы с ними. Такие движения редко отображаются в формулах, только в особых случаях. Рекомендуется начать сборку реберных граней с элементов нижних рядов, после таких вращений все нужные кубики спустятся из среднего в нижний ряд.
Составление второго креста
На четвертом этапе игрушку переворачивают “вверх тормашками”.
Решение последней грани – самая сложная часть алгоритма сборки кубика Рубика 3х3 для начинающих. Формулы вращений длинные и сложные, их выполнение потребует особой внимательности. Цель действий – расположить реберные элементы на своих места для дальнейшего составления креста. Ориентация реберных частей может быть неправильной. Формула движений кубика всего одна и применять ее следует пока не будет достигнута цель этапа. 

Вращения пятого этапа направлены на разворот элементов правильной стороной. Его особенность заключается в том, что применяется одна и та же формула вращения для всех узоров.
Формулы для движений 5 этапа выглядят следующим образом:
(ПСН)4 В (ПСН)4 В’ – вариант «А»;
(ПСН)4 В’ (ПСН)4 В – вариант «Б»;
СН – это поворот среднего ряда по часовой стрелке, а показатель степени над скобочкой – количество повторений действий в скобках.
Решение головоломки – последние вращения

Головоломку следует повернуть так, чтобы элемент, который уже на нужном месте, располагался в левом дальнем углу наверху кубика. Варианты, предложенные для решения формулы, зеркально отражают друг друга. Повторять вращения необходимо до достижения желаемого результата.

Шестой этап самый торжественный и самый трудный.
При вращениях кубика нарушения в уже собранных рядах неизбежны. Потребуется полностью сосредоточить внимание на движениях, иначе результат сборки может быть безвозвратно загублен. Как и в пятом этапе, последовательность движений всего одна, но повторяется по 4 раза. Сначала совершаются вращения для ориентации элемента, затем обратные – для восстановления нарушенных рядов. Не следует забывать о записи движений при помощи знаков английского алфавита. Формулы движений граней и рядов кубика данного этапа выглядят следующим образом: (RF’R’F)2 U (RF’R’F)2 – вариант «А»; (RF’R’F)2 U’ (RF’R’F)2 – вариант «Б»; (RF’R’F)2 U2 (RF’R’F)2 – вариант «В».
В – поворот верхней грани на 90 градусов, В’ – поворот той же грани против часовой стрелки, а В2 – двойной поворот. Сложность этапа в правильной оценке расположения элементов и выборе необходимого варианта вращений. Новичкам бывает трудно сразу правильно определить узор и сопоставить его с правильной формулой.
Рекорды по сборке кубика Рубика.
Научившись собирать кубик, я стала собирать его на время. Изначально у меня уходило на полную сборку около часа. Но с каждым разом получалось все лучше и лучше. (Приложение 4)
Но все же хочу приблизиться к мировым рекордам(Приложение 5)
А 45- летний британец Грэм Парк собрал кубик Рубика за 26 лет, но при этом он отказался от всех схем и алгоритмов сборки.
21 марта во Владивостоке прошли первые краевые соревнования по спидкубингу. Самой юной участнице соревнований Полине всего пять лет. Она даже в школу ещё не ходит, но уже собирает головоломку меньше чем за минуту. Иван Завгородний, житель Хабаровска, собирает кубик 3х3 за 3 секунды. Но так как это пробный вариант соревнований, т. е. соревнования не аккредитованы, то мировой рекорд не засчитан.
Заключение
И в заключение я хотела бы сказать, что математика применяется не только для вычисления разных формул и решения задач, но и для решения различных головоломок. Ведь именно математика помогла человеку найти секрет сборки «Кубика Рубика» за минимальное время. Благодаря изученному алгоритму сборки кубика, мне удается собрать кубик за 4 минуты. Тем самым мы частично опровергаем нашу гипотезу, т. е. не зная математики, можно собрать кубик, но на это уйдет огромное количество лет. Лучше понять алгоритм сборки и потратить на это несколько минут.
Но я не собираюсь останавливаться на достигнутом результате.
Я бы посоветовала всем родителям приобрести для своих детей головоломки Эрно Рубика, ведь чем раньше они начнут их решать, тем быстрее и лучше будет развиваться у них мыслительная деятельность.
Для тех, кто желал научиться собирать эту «детскую» на первый взгляд, головоломку, я оказывала посильную помощь, в результате среди моих одноклассников уже могут собирать одну, две грани кубика 3 учащихся, а полностью собирать кубик – 3 учащихся.
Для учащихся начальной школы, 8, 10, 11 классов проведены лектории по данной теме (Приложение 6).
На следующий год, хочу провести соревнования по скоростной сборке кубика Рубика (спидкубингу).
Список литературы
1.Сайт – Википедия . Кубик Рубика. https://ru.wikipedia.org/wiki/%D0%9A%D1%83%D0%B1%D0%B8%D0%BA_%D0%A0%D1%83%D0%B1%D0%B8%D0%BA%D0%B0
2. Сайт – «Нормы спорта и ГТО» https://gto-normativy.ru/mirovoj-rekord-po-sborke-kubika-rubika-3×3/
3.Сайт – «FB.ru». https://fb.ru/article/344145/algoritm-sborki-kubika-rubika-h-dlya-nachinayuschih-uzoryi-na-kubike-rubika-
4. Сайт – «Занимательная физика». https://www.afizika.ru/zanimatelniestati/174-kubikrubika
5. Сайт – «Вести Приморья». https://sport.rambler.ru/other/39418036-v-primore-proshli-sorevnovaniya-po-sborke-kubika-rubika-na-skorost/
Приложение № 1
Анкета
Знаете ли Вы, что такое кубик Рубика?___________________________
Известно ли Вам кто изобрел его?_______________________________
Пытались ли Вы когда-нибудь собирать кубик Рубика?______________
Удалось ли Вам полностью собрать кубик Рубика__________________
Приложение № 2
Результаты анкетирования учащихся МОУ Орлинская СОШ
Приложение № 3
Разновидности головоломок Эрно Рубика.
Название головоломки
Ее вид
Кубик Рубика
(от 2х2х2 до
11х11х11)

Пирамида Рубика

«Змейка» Рубика

Цилиндр Рубика

Шар Рубика

Различные
многогранники Рубика

Приложение № 4
Время сборки кубика Рубика
Приложение № 5
Хронология мировых рекордов кубика Рубика 3х3х3
Год
Рекорд
2013
В 2013 году голландскому подростку Мэтсу Валку удалось установить очередной рекорд скорости сборки классического кубика Рубика. На момент, когда все стороны этой механической головоломки окрасились в одинаковые цвета, секундомер фиксировал небывалый результат – всего 5,55 секунды.
2015
Поставленный Мэтсом Валком рекорд продержался не очень долго. Уже в апреле 2015 года очередному подростку из Америки удалось превзойти мирового лидера, собрав головоломку за рекордные 5,25 секунды. Тем самым за ним остался очередной рекорд.
2015
Но и это достижение продержалось недолго. Уже в ноябре 2015 года подросток из Амери?

